The m-Coloring problem concerns finding all ways to color an undirected graph using at most m different colors, so that no two adjacent vertices are the same color. We usually call the m-Coloring problem a unique problem for each value of m. An important application of graph coloring is the coloring of maps.
m-그래프 채색 문제는 비방향그래프에서 서로 인접한 정점이 같은 색을 갖지 않도록 최대 m개의 다른 색으로 칠하는 방법을 모두 찾는 것이다. m값에 대해서는 각기 다른 문제로 취급한다.
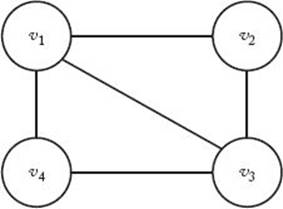
A graph is called planar if it can be drawn in a plane in such a way that no two edges cross each other. The graph at the below is planar. However, if we were to add the edges ($v_1$, $v_5$) and ($v_2$, $v_4$) it would no longer be planar. To every map there corresponds a planar graph. Each region in the map is represented by a vertex. If one region is adjacent to another region, we join their corresponding vertices by an edge. The below figure shows a map at the left and its planar graph representation at the right.
![[[Map(left) and its planar graph representation(right)]]](/images/algo/m-coloring.png)
2개의 이음선이 서로 교차하지 않도록 그린 그래프를 평면그래프라고 한다. 모든 지도는 그에 상응하는 평면그래프로 바꿔 그릴 수 있다. 지도에서 각 지역은 정점에 해당한다. 만일 한 지역이 다른 지역과 인접해 있으면, 그 정점들을 이음선으로 연결한다.
Example There is no solution to the 2-Coloring problem for this graph because, if we can use at most two different colors, there is no way to color the vertices so that no adjacent vertices are the same color. One solution to the 3-Coloring problem for this graph is as follows:
$$
\begin{align}
Ve&rtex &Color \\
&v_1 &color1 \\
&v_2 &color2 \\
&v_3 &color3 \\
&v_4 &color4
\end{align}
$$
There are a total of six solutions to the 3-Coloring problem for this graph. However, the six solutions are only different in the way the colors are permuted.
위의 그래프에서 최대 2개의 색만 사용할 수 있다면 인접한 정점이 같은 색을 갖지 않도록 칠하는 것은 불가능하다. 즉, 2-Coloring 문제에 대한 해답은 없다.
3개의 다른 색으로 그래프를 채색하는 경우 총 6가지 해답이 존재한다. 그러나 6가지 해답은 색이 조합된 방법만 다를 뿐이다.
The Backtracking Algorithm for the m-Coloring Problem
Algorithm Design
A straightforward state space tree for the m-Coloring problem is one in which
- each possible color is tried for vertex $v_1$ at level 1,
- each possible color is tried for vertex $v_2$ at level 2,
- and so on until each possible color has been tried for vertex $v_n$ at level n.
Each path from the root to a leaf is a candidate solution. We check whether a candidate solution is a solution by determining whether any two adjacent vertices are the same color.
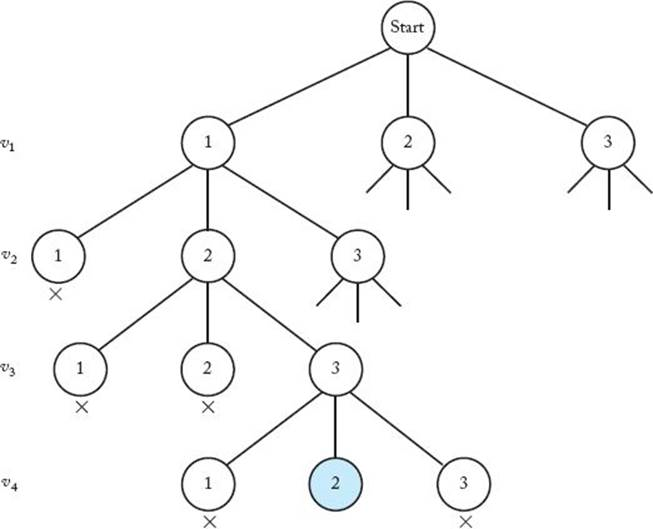
m-Coloring 문제에 대한 상태공간트리는 다음과 같다. 레벨 1에서 정점 $v_1$에 가능한 모든 색을 각각 시도하고, 레벨 2에서는 정점 $v_2$에 가능한 모든 색을 각각 시도해 본다. 이런식으로 레벨 n에서는 정점 $v_n$에 가능한 모든 색을 각각 시도해 본다.
상태공간트리의 루트노드에서 잎노드까지의 경로가 해답후보가 되며, 인접한 정점이 같은 색인지를 결정함으로써 해답여부를 판단한다.
We can backtrack in this problem because a node is nonpromising if a vertex that is adjacent to the vertex being colored at the node has already been colored the color that is being used at the node. After $v_1$ is colored color 1, choosing color 1 for $v_2$ is nonpromising because $v_1$ is adjacent to $v_2$. Similarly, after $v_1$, $v_2$, and $v_3$ have been colored colors 1, 2, and 3, respectively, choosing color 1 for $v_4$ is nonpromising because $v_1$ is adjacent to $v_4$.
한 정점에서 사용된 색이 인접한 정점을 칠하기 위해 사용됐다면 그 마디는 유망하지 않다. 이 점을 이용하면 이번 문제에서도 백트래킹을 적용할 수 있다. 예를 들어, $v_1$을 색1로 칠한 후 $v_2$에서 색1을 선택하는 것은 유망하지 않다. $v_1$과 $v_2$는 서로 인접해있기 때문이다. 마찬가지로 $v_1$, $v_2$, $v_3$를 색1, 색2, 색3으로 칠한 경우 $v_4$에서 색1을 선택하는 것은 유망하지 않다.
Pseudo Code
void m_coloring(index i) |
Source Code
// File: mcoloring.h |
// File: mcoloring.cpp |
// File: mcoloringtest.cpp |
Time Complexity Analysis
Worst-Case Time Complexity
- $O(n) = 1 + m + m^2 + m^3 + … + m^n = \frac{m^{n+1} - 1}{m-1} \in \Theta(m^n)$
For a given m and n, it is possible to create an instance that checks at least an exponentially large number of nodes (in terms of n). As with any backtracking algorithm, even though the worst case is exponential, the algorithm can be efficient for many large instances.
한 정점에서 가능한 모든 색(m개)을 시도해 봐야하므로 주어진 m, n에 대해 최소한 지수만큼 많은 노드의 수를 점검하는 상태공간트리를 만들 수 있다. 하지만 가지치기를 통해 상태노드의 수를 줄일 수 있기 때문에 알고리즘의 효율은 더 좋을 수 있다.
n-퀸 및 부분집합의 합 구하기 문제와 마찬가지로 유망한 노드의 수를 정확히 구하기 위한 방법은 실제 알고리즘을 수행 후 구축된 상태공간트리의 노드 갯수를 세어 보는 수 밖에 없다. 또한 몬테 카를로 알고리즘을 이용해 시간복잡도를 추정할 수 있다.